こんにちは、SEO/CRO担当のTAKITA(@tackey_cro)です。
今回から何回かに分けて、確率統計に関する記事を書きます。
このページを見ている方の多くはサイトの改善やデータ分析を主業務としている方だと思うのですが、それらの業務では確率統計の知識があることで、データをより定量的に評価できるようになるため、元理系の私の知見がお役に立てるのではないかと思います。(物理系専攻、大学院を修了。大手メーカーの元エンジニア)
確率統計の知識があると、例えば、ABテストの信頼性評価や、データの解釈、データから予測モデルを作成することなどが可能となりますので、最終的には上記のようなことができるようになることをゴールに設定して進めていきたいと思います。
ただ、
- 「数学って昔から苦手で…」
- 「数式が目に入ると読み飛ばしてしまう…」
- 「記号の意味が分からない…」
という方も多いかと思いますので、言葉の正確性よりもかみ砕いた表現を重視して説明します。
記号を導入する際も、例を交えながら丁寧に説明します。
また、より理解を深めたい方へ向けて、例題も用意してみましたので、余裕があれば取り組んでみてください。
なお、ABテストやデータ分析をアウトソーシングしたい場合はご相談ください。
確率とは
確率の考え方や場合の数について
簡単に言うと、確率とはある事象の起こりやすさのことです。
例えば、サイコロで1が出る度合や偶数が出る度合などが確率です。
式では、ある事象Xが起こる確率P(X)を下記のように表現します。
(※なお、これ以降、事象Xの要素をX={a,b,c,…}、その要素数(場合の数)をn(X)、起こる全ての事象Uの場合の数をn(U)と表記することにします。すると、事象Xの確率P(X)は、P(X)=n(X)/n(U)と表記できることになります。)
場合の数というのは、起こりうる事象が何パターンあるかということです。
サイコロの偶数が出る確率を求めるなら、偶数が出る場合の数は{2,4,6}の3通り、全ての起こる事象は{1,2,3,4,5,6}の6通りですね。
したがって、偶数が出る確率は3÷6=1/2 (50%)と求めることができます。
このように、場合の数を数えて割り算することで確率を求めるのですが、ここで1点注意点があります。
場合の数を数える場合、「同様に確からしい」ものを数える、という決まりがあります。
「同様に確からしい」とは
「同様に確からしい」というのは、起こりうる事象の起こりやすさが平等だということです。
…ってどういうこと?と疑問に持つ方が多いと思うので、具体例で説明します。
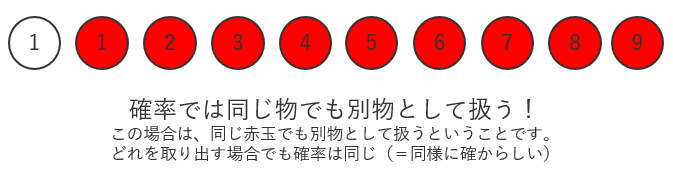
白玉1つと赤玉が9個入った袋から玉を1個だけ引く操作(試行)を行います。
この場合、白玉か赤玉のうちどちらかしか出ないから、白玉が出る確率は1/2だ!とするのは正しいでしょうか?
この理屈だと、赤玉が何個でも(1億個でも)白玉が出る確率は1/2だということになります。
でも赤玉が多ければ赤玉出やすそうですよね。
この例では、赤玉と白玉の個数が異なっており、色ごとの出やすさが平等ではないため誤りです。
何が平等かと考えると、色に関係なく各々の玉を引く確率が平等(等確率)ですよね(どの玉が出るかが同様に確からしい)。
この「同様に確からしい」というのは、玉すべてに番号を振って場合の数を数えるということを想像するとわかりやすいと思います(玉すべてを区別する)。
そうすることで、白と赤の2通りだ!という考えにはならず、白が1つ、赤が9個だということを認識しやすくなるかと思います。
実際、確率の世界では、全てのものを区別して数えるというルールがあります。
考えてみれば当たり前で、頭の中で赤玉を9個想像する場合は全て同じ赤玉かもしれませんが、目の前に赤玉が並んでいたらすべて区別できますよね。
ではここまでの内容の理解を深めるために、簡単な例題を解いてみましょう。
答え:1/10
白玉1、赤玉1~9と番号を付けたとします。
白玉を引く場合の数は、白玉1の1通り。(分子)
全事象の場合の数は白玉1、赤玉1~9の10通り。(分母)
したがって、1/10
場合の数を数える際に便利な道具や考え方
上記の例では、かなりシンプルなシチュエーションを設定したため、場合の数を数えるのは簡単だったと思います。
実際にはもっと複雑な操作を行う場合が多く、全パターンを1個ずつ数えるというのは非常に効率が悪いです。
そこで、場合の数を数える際に便利な道具を2つ紹介します。
順列
まずは順列という、物の並べ方が何通りあるかを計算する方法を説明します。
よく使うので、下記の具体例を通して、ぜひ理解していただければと思います。
その並べ方は何通りあるか?
答え:120通り
樹形図を書いて1つずつ数えてもいいのですが、階乗という方法で簡単に計算できます。
階乗とは、ある数(nとします)から1までの整数の積のことを言い、nの階乗をn!と表します。
n個のものをすべて使用した順列の場合の数はn!になるので、先ほどの例だと、5人の並べ方は5!=5×4×3×2×1=120通りとなります。
また、n個の中からk個だけ取り出して並べたい場合もあると思います。
それは記号Pを用いて\( {}_n \mathrm{P}_k \)と書き、\( \displaystyle {}_n P_k = n \times (n-1) \times \cdots \times (n-k+1) = \frac{n!}{(n-k)!} \)と計算します。
5人から3人選んで並べる場合の数は下記の通りとなります。
\( {}_5 \mathrm{P}_3 \ =5 \times 4 \times 3 \times 2 \times 1 \div (2 \times 1)=60 \)
組み合わせ
順列は並び順を気にしましたが、並び順を気にしない場合の数を求めることも多いと思います。
(複数のものからいくつか選択するだけの組み合わせしか気にしない場合)
この場合は、並び順が異なっていても組み合わせが等しいもの(並びを入れ替えると同じになるもの)は同一視します。
このような組み合わせを求める場合、n個のものからk個のものを取り出した場合の組み合わせ)、Cという記号を用いて\( {}_n \mathrm{C}_k \)と書き、\( \displaystyle {}_n C_k = \frac{n!}{k! (n-k)!} = \frac{{}_n P_k}{k!} \)と計算します。
答え:10通り
先ほどの計算をそのまま使って計算すると、
\( \displaystyle {}_5 C_3 = \frac{5!}{3! (5-3)!}\) = 10通り
となります。
その他、確率統計において覚えておきたいこと
これから何回かに分けて確率や統計の記事を投稿していきますが、その記事内で使用する用語や記号を8つ紹介します。
以下、それらについて1~6の目が出るサイコロを振るという試行を前提に、簡単な例とともに説明します。
全事象
起こりうるすべての事象を全事象と言い、Uという記号で表記します。
ある事象Xの要素(場合の数)をX={x1,x2,…}と表記することにすると、
サイコロの全事象は下記のように表記できます。
U={1,2,3,4,5,6}
積事象
事象Aと事象Bが同時に起こる事象を積事象(A∩Bと書く)と言います。
事象Aが1か3の目が出る事象(A={1,3})、事象Bが奇数の目が出る事象(B={1,3,5})だとすると、
事象Aと事象Bの積事象A∩Bは、
A∩B={1,3}
となります。
5が出る事象は事象Bにしか含まれておらず、事象Aと共通の事象ではないため除外されます。
和事象
事象Aまたは事象Bが起こる事象を和事象(A∪Bと書く)と言います。
事象Aが1か3の目が出る事象(A={1,3})、事象Bが奇数の目が出る事象(B={1,3,5})だとすると、
事象Aと事象Bの積事象A∪Bは、
A∪B={1,3,5}
となります。
空事象
起こりえない事象を空事象(記号φを使う)と言います。
例えば、サイコロでは7の目が出る事象や0の目が出る事象は起こりませんので、それらの事象は空事象であると言えます。
排反事象
事象Aと事象Bが同時に起こらないとき、事象Aと事象Bは互いに排反であると言います。(A∩B=φ)
A={1.2.3}
B={4,5,6}
のとき、事象Aと事象Bは排反です。
余事象
事象Aに対して、Aでない事象をAの余事象と言います。
例えば、サイコロを1つ振って、偶数が出る確率とその余事象を求める場合、
偶数は2,4,6の3通りでこの余事象は奇数の場合なので、1,3,5の3通り。
全事象数は6通りなので、偶数が出る確率は1/2、その余事象の確率も1/2となります。
求めたい事象に「少なくとも~~」という条件が入っている場合は、確率の合計が1(=100%)となることを活かして、余事象の確率を求めて1から引いたほうが簡単なので、覚えておきましょう。
答え:41/45
「白玉が少なくとも1つ取り出される事象」の余事象は「白玉が1つもない事象」です。
全て赤玉の場合の数は、8個の赤玉から2つ選ぶ組み合わせなので(順番関係なし)、\( {}_8 \mathrm{C}_2 = 4\)
分母は10個のものから2つ選ぶ組み合わせなので、\( {}_ {10} \mathrm{C}_2 = 45\)
よって求める確率は、1-4/45=41/45
条件付き確率
条件付確率というのは、「事象Bが起こったうえで、Bとは別の事象Aが起こる確率」のように、いくつかの事象がセットになった確率のことを言います。
これを \(P(A|B)=\frac{P(A \cap B)}{P(B)}\) と書きます。
1と書かれた白玉が1つ、1と書かれた赤玉が3つ、2と書かれた赤玉が6つ入っている袋から玉を1つ取り出した時、その玉は赤色でした。この赤い球に2と書かれている確率は?
答え:2/3
この問題では、「赤玉という条件のもと、1を引く確率」を求めることになります。これを条件付確率で求めます。
事象A:1を引く
事象B:赤玉を引く
として、事象Bが起こったうえで事象Aが起こった確率を求めます。
P(B)=9/10 (赤玉は10個中9個)
P(A∩B)=3/5 (2と書いてある赤玉は10個中6個)
よって、\(P(A|B)=\frac{P(A \cap B)}{P(B)} = \frac{3/5}{9/10} =2/3\)
期待値
期待値は、ある試行で得られる数値の平均値です。
得られる可能性がある値とそれが起こる確率を掛け算して、全て足したものが期待になります。
1回300円で買える福引において、賞金とその確率が下記のように定まっている場合の期待値は?また、この宝福引は買うべきだろうか?
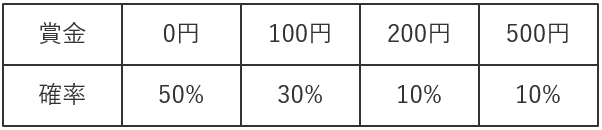
期待値は、0×0.5+100×0.3+200×0.1+500×0.1=100円 となる。
これは、福引を1回買うごとに平均的に100円得られることになる。
しかし、福引は1回300円で購入するため、福引1回挑戦するごとに平均200円失うことになる。
したがって、この福引は買うべきではない。
まとめ
慣れない記号も出てきて少し大変だったかもしれません。
ただ、今回の内容を理解できていれば、確率の超基本的な事項については理解できたと言っていいと思います。
多少わからないことがあったとしても、例題を読んだり解いたりすることで理解が深まっていくと思いますので、時間があるときに例題にも目を通して見てください。
そして、徐々に理解を深めていきつつ、このシリーズのゴールである確率統計を仕事に生かすというところまで到達いただければと考えております。
アイオイクスではSEOを軸としたWebコンサルティングサービスを提供しています。
いわゆるSEOの型に沿った施策ではなく、お客様の事業やWebサイトの構成を踏まえた最適な施策のご提案を重要視しています。SEOにお困りの際はぜひご相談ください。
→SEOコンサルティング サービスページ
アイオイクスでは一緒に働く仲間を募集しています
アイオイクスのWebコンサルティング事業部では、「一緒に挑戦し、成功の物語を共有する」という理想像を掲げ、本質的な取り組みを推進しています。私たちと汎用性の高いスキルを突き詰め、自由に仕事をしていきませんか。
メールマガジンの登録はこちら
SEOに関連する記事の更新やセミナー情報をお届けします。








