ABテストやデータ分析で役に立つ確率統計②確率分布や正規分布

こんにちは、SEO/CRO担当のTAKITA(@tackey_cro)です。

前回の記事(確率の基本)では、確率の基本的な考え方や用語について紹介しました。

今回は、統計でよく使われる確率分布について紹介します。
特に、仮説検定で用いられる正規分布は非常に重要なので、ぜひご理解いただきたいと思います。

ただし、前回よりは少し難しいかもしれません。
できるだけ図解を多くし分かりやすくなるように努めましたが、もし難しければツイッターにご連絡ください。

確率分布とは？

まずは確率分布について説明しますが、その前に以下の用語を確認してください。

確率：事象の起こりやすさ
確率変数：確率によって起きうる事象が取る変数

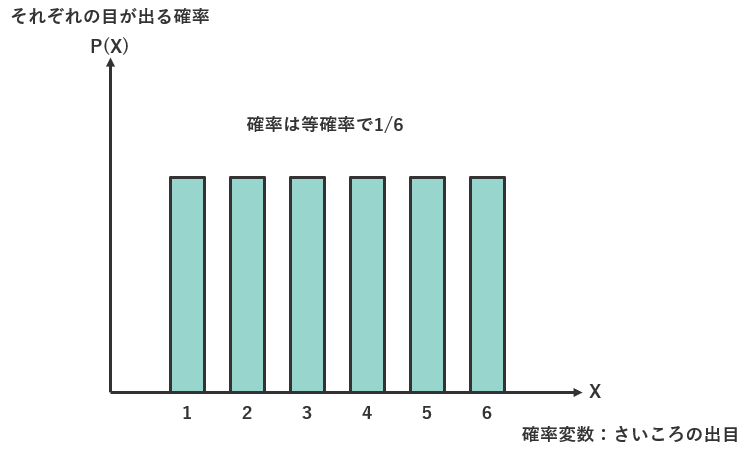
例えば、1～6の目が出るサイコロを振ることを考える場合、1～6が確率変数に該当します。
確率は、それぞれの目が出る確率なので、この場合は1/6です。

約束事として、確率変数Xの確率をP(X)のように表記することとします。
サイコロの例だと、P(1)=1/6というように書きます。

上記のような、確率変数を横軸、確率を縦にしてグラフにしたものを確率分布と言います。

確率分布には、確率変数が取りうる値によって、離散型確率分布、連続型確率分布のいずれかに分けられます。
これら2種類の分布について説明しますが、統計では連続型確率分布のほうが重要なので、そちらを重点的に説明します。

離散型確率分布

1~6の目が出るサイコロのように、確率変数がとびとびの値をとる場合の分布を離散型確率分布と言います。(離散型というのはとびとびという意味です)
サイコロの場合、確率変数が1、2、3、4、5、6と自然数の値しかとりません。
しかし、各自然数の間には小数が存在していて、それらの値を確率変数に含まないため、サイコロは離散型確率分布といえます。

離散型確率分布では、その分布を表す確率密度関数がP(X)であり、確率P(X)と同じ形をしています。
これは、確率変数を1つ決めるとそれに対応する確率が決まる、という離散型確率分布の特徴に起因しています。

連続型確率分布

一方、連続型確率分布は自然数やその間の小数も全て確率変数になります。
例えば、1と2の間には1.1や1.2が存在していて、さらにその間には1.11、1.12…と数が無限個存在していて、これらすべてが確率変数となります。
このように、無限個の変数をとる分布が連続型確率分布です。

連続型確率分布の重要な性質として、ある特定の確率変数の確率はゼロになる、というものがあります。

離散型確率分布では確率変数が有限個であったため、任意の確率変数に対する確率が定まりました。
しかし連続型確率分布では、確率変数が無限個であるため、任意の確率変数に対する確率は、分母が無限大となるためゼロとなります(1/∞=0)。

そのため連続型確率分布では、確率密度関数f(x)をある一定区間積分することで確率を求めます。
言い換えると、確率は確率変数の範囲によって定められるということです。

また、上記の事から、離散型確率分布では確率変数に対して確率が対応していましたが、連続型確率分布では、確率変数に対して確率密度関数が対応している点に注意してください。

正規分布

確率や統計でよく用いられる連続型確率分布に正規分布というものがあります。

正規分布の広く知られた特徴として、自然会や社会で起きる事象が正規分布になりやすい、ということがあり、正規分布は最も頻繁に利用される確率分布の1つです。

また、中心極限定理(後述)によって、ほとんどの標本平均の確率分布が正規分布に近似可能です。これも正規分布が用いられる理由です。

中心極限定理
「母集団の分布に依存せず、標本数が大きくなると、標本平均の分布が平均μ、分散σ^2/nの正規分布に近づく」というものが中心極限定理です。
中心極限定理を用いると、標本数が大きくなるにつれて分散が小さくなるため平均値を求めやすくなるというメリットがあります。

統計や検定の話の際に、正規分布の知識を既知としますので、以下の正規分布の特徴を抑えておいてください。

1. 連続型確率分布である
2. 平均値と最頻値と中央値が一致する
3. 左右対称
4. 横軸に漸近する(限りなく近づく)
5. 確率変数の個数は無限大
6. 確率変数は-∞から＋∞の実数をとる
7. 5の全範囲で積分すると1になる(確率の合計は1)
8. 分散(標準偏差)が大きくなると山がなだらかに、小さくなるとシャープになる

正規分布と標準偏差

正規分布を扱う上で重要な指標が標準偏差です。
標準偏差σは、分散σ^2を1/2乗した指標で、平均値と同じ次元(単位)となるため、分散よりも扱いやすいという特徴があります。

例えば、成人男性の平均体重が65kg、標準偏差σが3kgの場合、約68%の男性が65±3kgの体重だということがわかります。

ここで、68%という数字がどこから出てきたかが気になることと思います。
正規分布と標準偏差には下図のような関係があり、1σ区間に入っているデータの割合が全体の68%、2σ区間なら約95%、3σ区間なら99.7%となります。

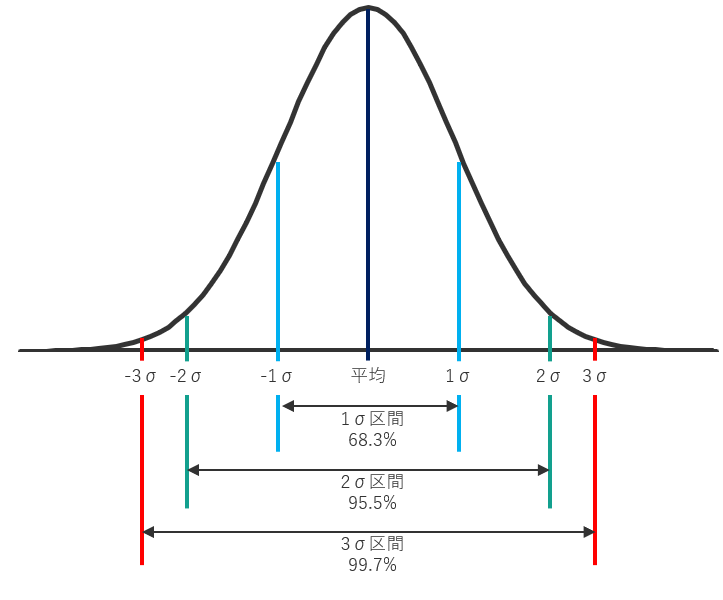
これらの区間の内、習慣的に2σ区間を採用するケースが多く、2σ区間に入っていればメジャーなケース、2σ区間の外である5%に入っていればレアなケースと判断します。

この考え方は統計の仮説検定で使いますので、覚えておきましょう。

正規分布の標準化

正規分布は、取得するデータによってさまざまな値を取りますが、データにある値をかけたり引いたりすることで、ただ一つの正規分布に変換することができます。
これを正規分布の標準化と言い、標準化後の正規分布を標準正規分布と言います。

この操作を行うことで、どんな正規分布であっても標準正規分布を考えることで、ある区間に属するデータ数を求めるなどが可能となります。

なお、データの変換は下記のように行います。
正規分布の確率変数がX、平均がμ、分散がσのとき、変換後のデータzは

z=(X-u)/σ

によって変換でき、平均が0、分散が1の標準正規分布が得られます。

正規分布を用いた例：偏差値

学生時代に、偏差値によって自分の学力を確認していた方は多いと思います。
偏差値50が平均くらいで、60を超えればそこそこ良く、40を切れば悪いというイメージがあるかと思います。
この偏差値は、正規分布や標準正規分布を用いて導くことができます。

偏差値の分布は標準正規分布を求めたうえで、平均値が50、標準偏差が10となるように調整された分布になっているため、標準化後のデータzに対し、

z’=z×10+50

という変換を行って分布を作ります。

このグラフを見ればわかるように、1σ区間内は全体の7割近くの人が含まれるため、比較的平凡な偏差値だと言えるでしょう(例えば、偏差値57程度であればそれほど珍しくはありません)。

1σ以上(60以上)からは全体の約16%であるため、比較的優秀と言えます。
2σ以上(70以上)は全体の約2.5%なので、かなり優秀ですね。

実際、偏差値70以上は非常に優秀というイメージがあると思いますが、そのイメージはこのように定量的に説明できるわけです。

ちなみに、グラフの左側では全く逆のことが言えます。

まとめ

今回は主に正規分布について紹介しました。
正規分布を理解すると、データの分析が出来るようになりますし、ABテストの有意差を評価することもできるようになります。

少し大変かもしれませんが、ぜひご理解いただきたいと思います。

分からなかったところはツイッターに連絡いただければ、時間を見つけて対応したいと思います。